春节后巩固学习：用解常微分方程组模拟抛体运动的详细教程

春节假期刚刚结束，人们仍沉浸在走亲访友的喜悦之中。然而，对于许多人而言，学习是不能放松的，春节期间的学习内容可能会变得生疏。例如，“解常微分方程组”这类技术性较强的知识，只有持续巩固，才能取得理想的效果。

春节探亲后的学习状态

春节期间，走访亲友，感觉时间飞逝。这源于我国传统节日的独特魅力，人们沉浸在团圆的喜悦中。我自然也不例外，去了岳母家，还拜访了其他亲戚。然而，这样一来，之前学过的知识似乎都被抛诸脑后。就拿“解常微分方程组”来说，感觉记忆已经模糊不清。为了更好地掌握这些知识，我不得不重新开始复习和实践。

重新开始学习知识并不容易。人脑在享受休闲和娱乐之后，往往会对学习产生一定的抵触情绪。然而，考虑到后续的学习和工作可能需要运用这些知识，比如在模拟物体运动时，我们就必须努力克服这种困难。

抛体运动的理论模型

抛体运动在理论上是典型的运动模型。举例来说，像扔铅球这样的体育活动，其运动轨迹与抛体运动相似。抛体运动仅受重力影响，其加速度方向为垂直向下。若将向上方向设为正，则加速度表达式为ay = -g。这里的g值大约是9.8米每二次方秒，而在地球上不同地点，由于重力加速度的细微差异，这个值会有所不同，尤其是在高海拔地区，这个值会相对较小。

为了找出抛体运动的路径，我们必须列出四个微分方程。这四个方程能详尽地展现抛体在平面上的位置和速度如何随时间变化。只有准确无误地写出这些方程，我们才能借助解常微分方程组的命令，获得精确的答案。

课件制作的关键步骤

制作课件时，首先要确定初始值。这些初始值，比如位置和速度，对于整个过程至关重要，就好比游戏开始时的基本设置。比如，如果我们把一个物体水平初速度设为6米每秒，这就构成了我们的初始条件。随后，我们将基于理论分析得出的四个微分方程输入指令栏，输入类似“求解常微分方程组({x', y', v_x', v_y'}, 0, {x_0, y_0, v_x_0, v_y_0}, 30)”的命令，就能获得四个解。

解出结果后，接下来是描点绘图。具体操作是，通过指令在方程的四个解上实施描点。例如，提取相应的纵坐标，从而获得坐标和速度的具体数值。绘制速度矢量时，遵循特定的公式，比如“向量(C, C+(0.3y(D), 0.3y(E)))”。此外，将速度调整为真实值的0.3倍，这样的比例在课件展示中更为适宜。

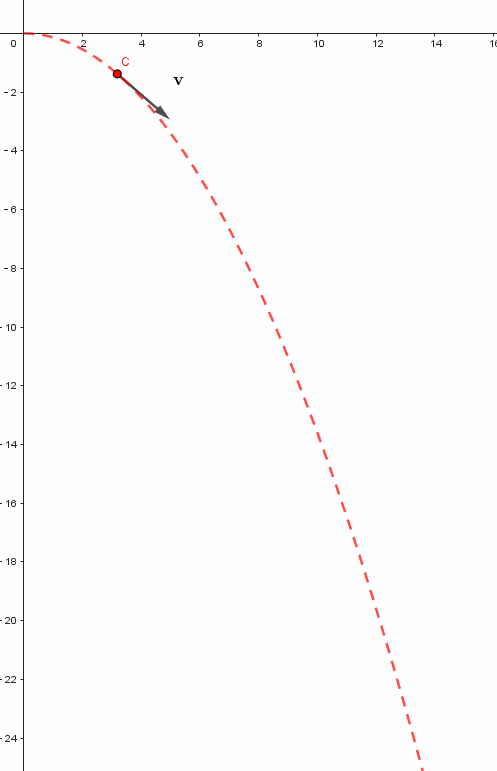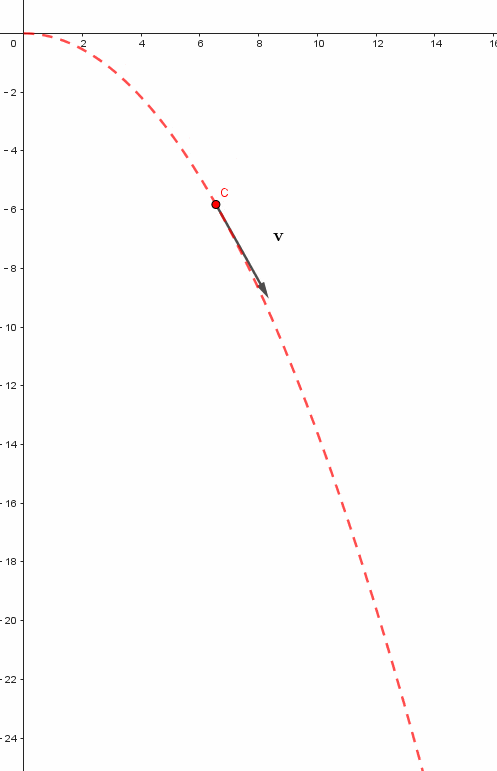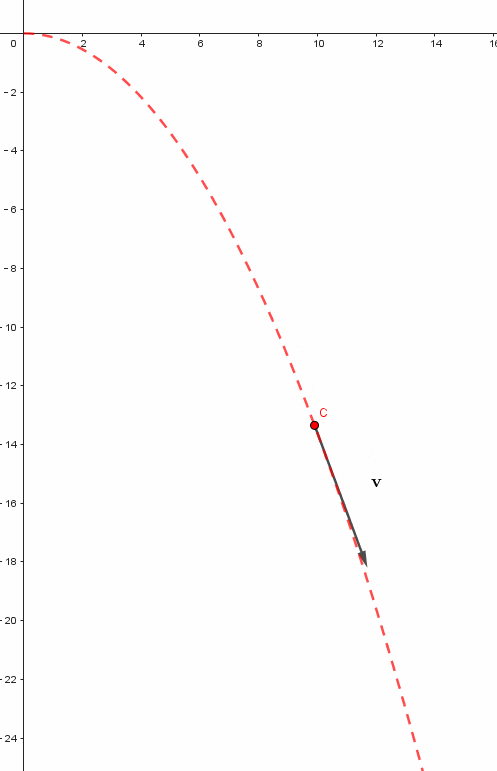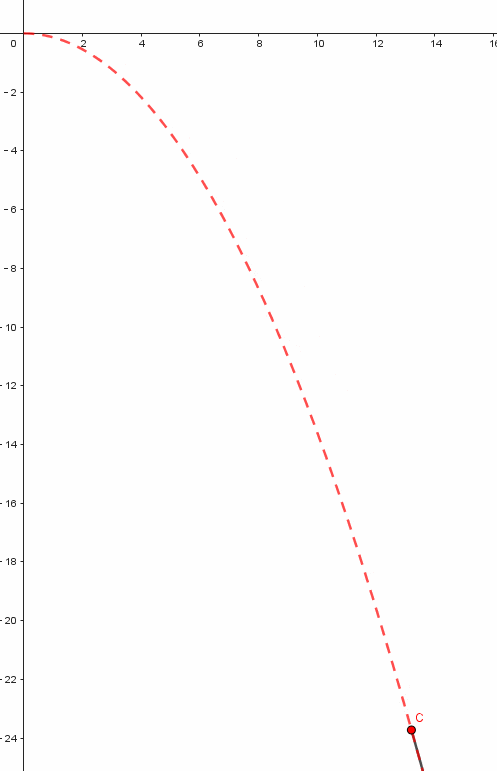
平抛运动模拟

模拟平抛运动的过程较为规律。我们设定了水平初速度为6。在日常生活中，平抛现象屡见不鲜，例如将一个物体从桌上水平抛出。确定水平速度后，依据先前的理论分析和课件制作步骤，通过求解常微分方程组，可以计算出物体在不同时间点的位置坐标、速度的大小和方向等详细信息。

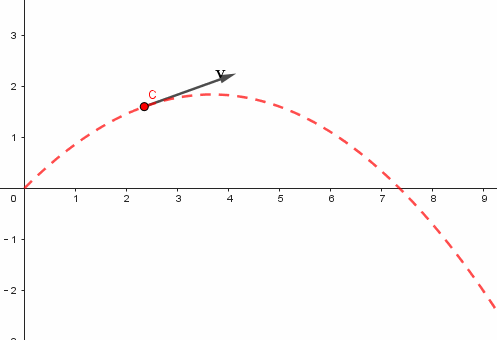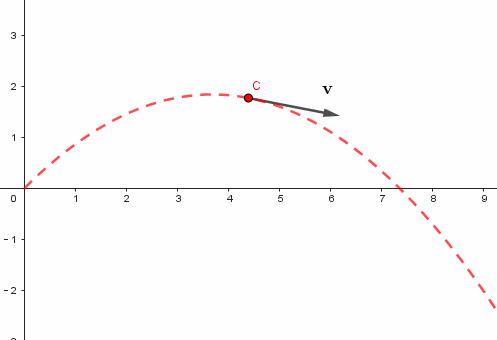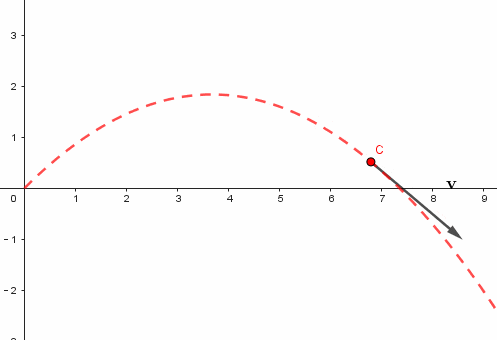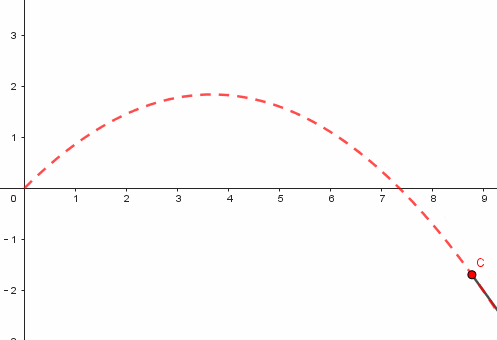
这些数据在图表上直接呈现为一条曲线。这条曲线描绘了物体在平抛运动中的运动路径。通过这条路径，我们可以清晰地观察到物体是如何遵循物理定律在空间中移动的。

斜抛与竖抛运动

生活中存在类似飞镖在空中飞行的斜抛运动情形。斜抛运动的轨迹会因初速度的不同而有所区别。比如，当水平初速度和竖直初速度均为6时，轨迹与水平初速度为6、竖直初速度为10时的轨迹就不同。在竖直上抛运动中，若水平初速度为0、竖直初速度为8，这便类似于向上抛球。而竖直下抛运动，若水平初速度为0、竖直初速度为-5，则类似于从高处扔下物体。

不同情况下，解出的微分方程描绘出的曲线各不相同。这些曲线展现了速度和位置的各异变化，有助于我们深入把握各类抛体运动的特性。